Multinode PyTorch Model Training using MPI and Singularity
Why multiple nodes?
Multinode training in PyTorch allows for the distribution of the computational workload across multiple nodes, which results in faster model training and increased scalability. By leveraging multiple nodes, each with its own set of resources, the data can be partitioned, and computations performed in parallel, leading to improved performance. Additionally, multinode training enables the training of larger models with more data, which may be impractical or impossible to train on a single node.
Why HPC?
HPC systems typically have more processors per node. Each node can handle more parallel processing power, reducing the need for additional nodes. This can help to reduce network latency, as fewer nodes need to communicate with each other during the training process.
Another advantage is the fast InfiniBand connectivity between nodes, which enables efficient communication and coordination between nodes during the training process. This is essential for maintaining synchronization and consistency across the distributed system. OAsis currently provides an inter-node bandwidth of 100 Gbps.
Moreover, HPC systems offer immediate access to high-performance computing resources without waiting for virtual machines to start. This means that users can start training their models immediately, eliminating any potential delays.
Why MPI?
MPI (Message Passing Interface) is a reliable, efficient, and widely adopted standard for parallel processing that enables communication between multiple nodes in a distributed system. MPI is a good choice for multinode PyTorch model training because it provides a standardized way for nodes to communicate and synchronize their work, critical for ensuring model accuracy and consistency.
MPI can handle both synchronous and asynchronous communication, allowing for efficient data transfer and synchronization between nodes. MPI also provides fault tolerance features, essential when working with distributed systems, ensuring the training can continue even if one or more nodes fail.
Why Singularity (containers)?
Singularity is a containerization tool that enables users to run applications in a self-contained environment. It provides a consistent and reproducible environment across all nodes. This eliminates the need for manual installation and configuration of software on each node, reducing the risk of version incompatibilities and errors.
Singularity also provides security benefits, as the containerized environment is isolated from the host system. This ensures that any potential security vulnerabilities or conflicts with other software on the host system do not affect the training process.
Setup
In this article, we will discuss how to train a PyTorch Distributed Data Parallel (DDP) model on 3 nodes, each with 16 CPU cores, to approximate an arbitrary polynomial function. The DDP technique is a powerful tool for distributed training of deep learning models that allows us to distribute the workload across multiple nodes while maintaining model accuracy and consistency. The 3 processes will be communicating with each other with the MPI.
We require two files; the main Python script, main.py, and a job description file run.sbatch. It would be best to group them into a folder for better organization.
# $HOME/pytorch-mpi-singularity/main.py
import numpy as np
import torch
import torch.distributed as dist
import torch.nn as nn
import torch.optim as optim
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
import socket
from torch.nn.parallel import DistributedDataParallel as DDP
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.fc1 = nn.Linear(1, 20)
self.fc2 = nn.Linear(20, 1, bias=False)
self.tanh = nn.Tanh()
def forward(self, x):
return self.tanh(self.fc2(self.fc1(x)))
def myfun(x):
return (np.power(x, 3) + np.power(x-10, 4))/np.power(x-20, 2) # polynom
# return 1+np.power(x,2)/4000-np.cos(x) # Griewank function
epochs = 1000
batch_size = 32
x_train = np.linspace(-3, 10, num=batch_size).reshape(-1, 1)
y_train = myfun(x_train)
x_scaler = MinMaxScaler(feature_range=(-1, 1))
y_scaler = MinMaxScaler(feature_range=(-1, 1))
x_scaled = x_scaler.fit_transform(x_train)
y_scaled = y_scaler.fit_transform(y_train)
x_eval = np.linspace(-3, 10, num=batch_size).reshape(-1, 1)
y_eval = myfun(x_eval)
x_eval_scaled = x_scaler.transform(x_eval)
x_eval_tensor = torch.from_numpy(x_eval_scaled).float()
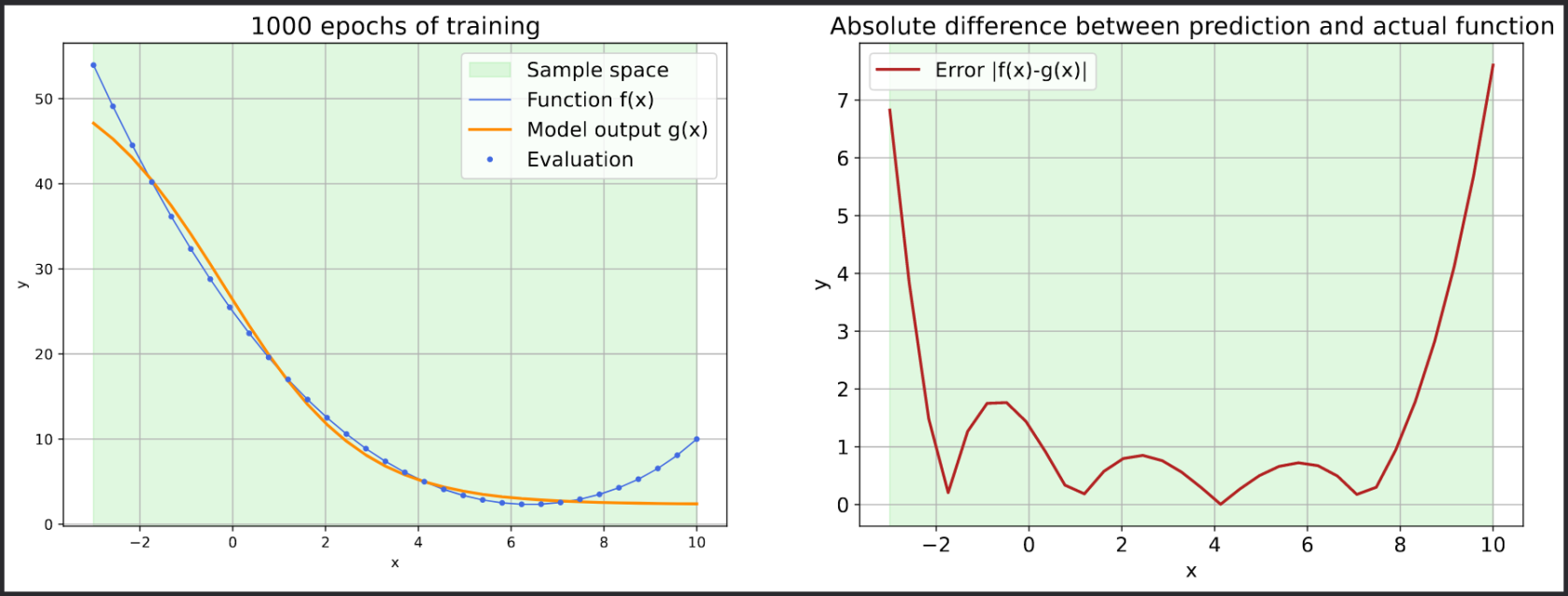
def plot_1d_function(predictions, total_epochs):
fig = plt.figure(1, figsize=(18, 6))
ax = fig.add_subplot(1, 2, 1)
ax.axvspan(x_train.flatten()[0], x_train.flatten()[-1], alpha=0.15, color="limegreen")
plt.plot(x_eval, myfun(x_eval), '-', color='royalblue', linewidth=1.0)
plt.plot(x_eval, predictions, '-', label='output', color='darkorange', linewidth=2.0)
plt.plot(x_train, myfun(x_train), '.', color='royalblue')
plt.grid(which='both')
plt.rcParams.update({'font.size': 14})
plt.xlabel('x')
plt.ylabel('y')
plt.title('%d epochs of training' % (total_epochs))
plt.legend(['Sample space', 'Function f(x)', 'Model output g(x)', 'Evaluation'])
ax = fig.add_subplot(1, 2, 2)
ax.axvspan(x_train.flatten()[0], x_train.flatten()[-1], alpha=0.15, color='limegreen', label='_nolegend_')
plt.plot(x_eval, np.abs(predictions-myfun(x_eval)), '-', label='output', color='firebrick', linewidth=2.0)
plt.grid(which='both')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Absolute difference between prediction and actual function')
plt.legend(['Error |f(x)-g(x)|'])
plt.savefig('errors.pdf', bbox_inches='tight')
print(f"plot evaluation result to errors.pdf")
def run(rank, size):
print(f"Running DDP on rank {rank}/{size}.")
model = Model()
ddp_model = DDP(model)
loss_fn = nn.MSELoss(reduction='mean')
optimizer = optim.Adam(ddp_model.parameters(), lr=0.001)
for epoch in range(epochs):
x_train = torch.rand(batch_size, 1) * 13 - 3
y_train = myfun(x_train)
x_train = x_scaler.transform(x_train)
y_train = y_scaler.transform(y_train)
x_train = torch.from_numpy(x_train).float()
y_train = torch.from_numpy(y_train).float()
yhat = ddp_model(x_train)
loss = loss_fn(yhat, y_train)
loss.backward()
optimizer.step()
optimizer.zero_grad()
if epoch % 100 == 0:
hostname = socket.gethostname()
print(f"epoch {epoch}, loss = {loss}, rank {rank}/{size} ({hostname}).")
if rank == 0:
yhat_eval = ddp_model(x_eval_tensor)
result_eval = yhat_eval.detach().cpu().numpy()
res_rescaled = y_scaler.inverse_transform(result_eval)
plot_1d_function(res_rescaled, epochs)
if __name__ == "__main__":
dist.init_process_group("mpi")
rank = dist.get_rank()
size = dist.get_world_size()
run(rank, size)
dist.destroy_process_group()#!/usr/bin/env bash
# $HOME/pytorch-mpi-singularity/run.sbatch
#SBATCH -J pytorch-mpi-singularity
#SBATCH -o pytorch-mpi-singularity.out
#SBATCH -e pytorch-mpi-singularity.out
#SBATCH -p batch
#SBATCH -t 5
#SBATCH -n 3
#SBATCH -c 16
#SBATCH -N 3
#SBATCH --mem=64G
module load GCC/11.3.0 OpenMPI/4.1.4
mpiexec singularity exec /pfss/containers/ngc.pytorch.22.09.sif python main.pyAs indicated in the sbatch file, we have requested three processes on three distinct compute nodes, with each process allocated three CPU cores and 64GB of memory. The job will be put into the batch queue and cannot run for more than 5 minutes.
Now we may submit the job to the HPC cluster. Our model is relatively simple, and it should complete within 10 seconds. Once the job is completed, we can review the output contained in the pytorch-mpi-singularity.out file.
sbatch run.sbatch
tail -f pytorch-mpi-singularity.out
# Running DDP on rank 1/3.
# Running DDP on rank 0/3.
# Running DDP on rank 2/3.
# epoch 0, loss = 0.6970552802085876, rank 0/3 (cpuamdg10001).
# epoch 0, loss = 0.6552489995956421, rank 1/3 (cpuamdg10002).
# epoch 0, loss = 0.613753080368042, rank 2/3 (cpuamdg10003).
# epoch 100, loss = 0.15419788658618927, rank 0/3 (cpuamdg10001).
# epoch 100, loss = 0.13655585050582886, rank 1/3 (cpuamdg10002).
# epoch 100, loss = 0.12928889691829681, rank 2/3 (cpuamdg10003).
# epoch 200, loss = 0.04900356009602547, rank 0/3 (cpuamdg10001).
# epoch 200, loss = 0.040532443672418594, rank 1/3 (cpuamdg10002).
# epoch 200, loss = 0.04361008480191231, rank 2/3 (cpuamdg10003).
# epoch 300, loss = 0.020832832902669907, rank 0/3 (cpuamdg10001).
# epoch 300, loss = 0.01722469925880432, rank 1/3 (cpuamdg10002).
# epoch 300, loss = 0.02464170753955841, rank 2/3 (cpuamdg10003).
# epoch 400, loss = 0.014773314818739891, rank 0/3 (cpuamdg10001).
# epoch 400, loss = 0.012860079295933247, rank 1/3 (cpuamdg10002).
# epoch 400, loss = 0.010255211964249611, rank 2/3 (cpuamdg10003).
# epoch 500, loss = 0.006024891510605812, rank 0/3 (cpuamdg10001).
# epoch 500, loss = 0.010885883122682571, rank 1/3 (cpuamdg10002).
# epoch 500, loss = 0.01051397155970335, rank 2/3 (cpuamdg10003).
# epoch 600, loss = 0.005216504912823439, rank 0/3 (cpuamdg10001).
# epoch 600, loss = 0.007366226986050606, rank 1/3 (cpuamdg10002).
# epoch 600, loss = 0.0031539099290966988, rank 2/3 (cpuamdg10003).
# epoch 700, loss = 0.008166833780705929, rank 0/3 (cpuamdg10001).
# epoch 700, loss = 0.012004977092146873, rank 1/3 (cpuamdg10002).
# epoch 700, loss = 0.004705417435616255, rank 2/3 (cpuamdg10003).
# epoch 800, loss = 0.005532342940568924, rank 0/3 (cpuamdg10001).
# epoch 800, loss = 0.007162642199546099, rank 1/3 (cpuamdg10002).
# epoch 800, loss = 0.007548379711806774, rank 2/3 (cpuamdg10003).
# epoch 900, loss = 0.004862943198531866, rank 0/3 (cpuamdg10001).
# epoch 900, loss = 0.007574871182441711, rank 2/3 (cpuamdg10003).
# epoch 900, loss = 0.006178494542837143, rank 1/3 (cpuamdg10002).
# plot evaluation result to errors.pdfBy accessing the web portal, you can monitor the efficiency of the job in terms of memory and CPU usage. Additionally, you can view the errors.pdf file via the file browser, which displays the error decline for each epoch.